Berechne folgendes Kreisbogenvieleck
Aufgabe
Berechne den Flächeninhalt der grün markierten Figur.
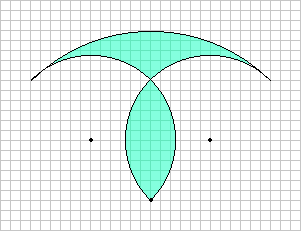
Lösung
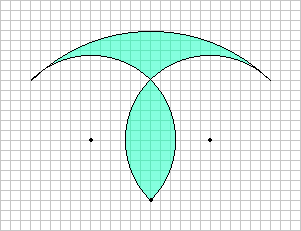
| Zunächst ist zu klären, aus welchen Teilstücken sich die Figur zusammensetzt. |
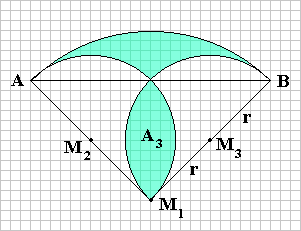
| Durch das Einzeichnen der Hilfslinien AM1, BM1
und AB kann abgelesen werden:
A1: Sektor, Mittelpunkt M1, Radius 2r, Mittelpunktswinkel 90° A2: Sektor, Mittelpunkte M2 und M3, Radius r, Mittelpunktswinkel 180° Man erhält für die gesuchte Fläche A: A=A1-2·A2+A3 |
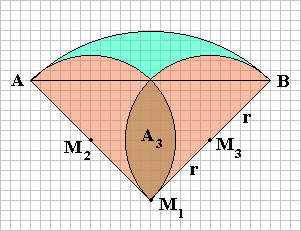
| Allerdings hat man so die mit A3 bezeichnete
Fläche 2-mal subtrahiert, da sie in beiden mit A2 bezeichneten
Flächeninhalten enthalten ist; diese Fläche ist demnach 1-mal
dem Ergebnis zuzuschlagen:
A=A1-2·A2+A3+A3 A=A1-2·A2+2·A3 |
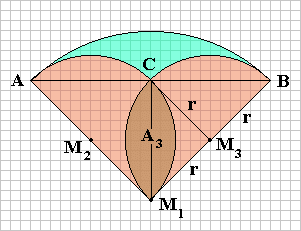
| Die Strecke M1C teilt A3 in zwei gleich
große Teile. Beide Teile setzen sich folgendermaßen zusammen:
A4: Sektor, Mittelpunkt M3 bzw. M2, Radius r, Mittelpunktswinkel 90° A5: Dreieck M1M3C bzw. M2M1C, Grundseite = Höhe = r Es ist:
und damit: A=A1-2·A2+2·2·(A4-A5) A=A1-2·A2+4·(A4-A5) |
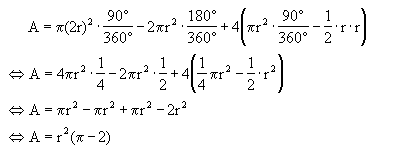 |
zurück zur Übersicht Kreisbogenvielecke
Lerninhalte zum Thema Kreis findest du auf dem Lernportal Duden Learnattack.
Mit Duden Learnattack bereiten sich Schüler optimal auf Mathematik Klassenarbeiten vor.
Interessante Lerninhalte für die 10. Klasse:
