Potenzfunktionen anhand eines Graphen bestimmen
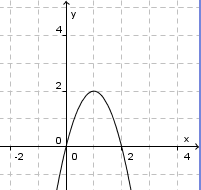
Welche der angegebenen Funktionsgleichungen passt zum Graphen? Begründe deine Wahl!
Aufgabe
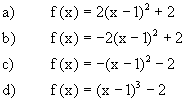
Lösung
Bei dem Graphen handelt es sich um eine nach unten geöffnete Parabel. Daher muss es sich um eine Potenzfunktion mit positivem Exponenten handeln. Da die Parabel achsensymmetrisch ist, muss der Exponent eine gerade Zahl sein. Die Lösung d) kann man also ausschließen.
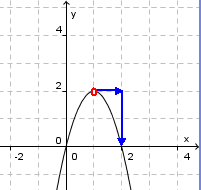
Der Scheitelpunkt hat die Koordinaten (1|2), d.h. der Graph ist gegenüber dem Graphen der Grundfunktion um 1 Einheit nach rechts und um 2 Einheiten nach oben verschoben. Von diesem Scheitelpunkt aus betrachtet gelangt man zu dem Punkt des Funktionsgraphen, dessen x-Koordinate um 1 größer ist als die des Schnittpunktes, indem man 2 Einheiten nach unten geht. Der Graph der Funktion ist daher mit dem Faktor 2 gestreckt und gespiegelt worden.
Demnach kommt nur Lösung b) in Frage!
zurück zur Übersicht Potenzfunktionen
Lerninhalte zum Thema Potenzfunktionen findest du auf dem Lernportal Duden Learnattack.
Mit Duden Learnattack bereiten sich Schüler optimal auf Mathematik Klassenarbeiten vor.
Interessante Lerninhalte für die 10. Klasse:
