zurück
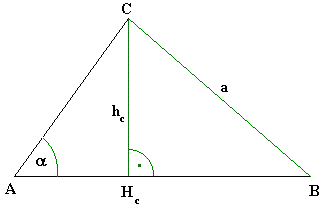
Konstruiere ein Dreieck aus a=3,8 cm; α=50°; hc=3,6 cm
| Punkte |
festgelegt durch |
| A, Hc, C |
SWW |
| B |
- s(AHc)
- K(C,a)
|
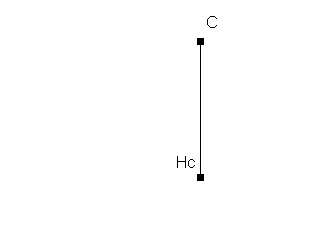 |
- Zeichne die Strecke CHc mit hc=3,6 cm
- Errichte die Senkrechte in Hc zur Strecke CHc.
- Lege auf der Senkrechten einen Punkt A' beliebig fest
- Trage in A' an A'Hc den Winkel α=50° an
- Zeichne eine Parallele zum freien Schenkel des Winkels α durch C
- Der Schnittpunkt des freien Schenkels des Winkels γ mit dem Strahl s(HcA') ist der Punkt A
- Zeichne einen Kreis um C mit dem Radius a=3,8 cm
- Der Schnittpunkt des Kreises mit dem Strahl s(AHc) ist B
- Teichne die Strecke BC
- ABC ist das gesuchte Dreieck.
|
Fehlende Größen:
b = 4,7 cm
c = 4,2 cm
β = 71,3°
γ = 58,7°



