Konstruiere ein Drachenviereck aus e=6 cm; f=4 cm; β=102°

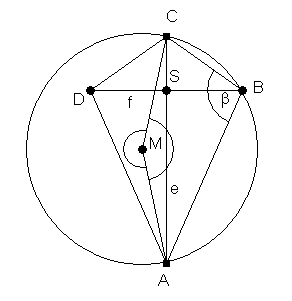
In einem Drachenviereck halbiert die Symmetrieachse die zweite Diagonale. Hier gilt also: SB = 4 cm : 2 = 2 cm.
Betrachtet man β als Umfangswinkel über AC, dann ist M ist der Mittelpunkt des Kreises, dessen Umfangswinkel über AC das Maß 102° haben. Der zugehörige Mittelpunktswinkel hat dann das Maß 2β=204°.
Das Maß des Winkels AMC beträgt nach 360° - 204° = 156°
Das Dreieck ACM ist gleichschenklig, da MA und MC Kreisradien darstellen. Also können die Basiswinkel nach dem Innenwinkelsatz für Dreiecke berechnet werden:

Zeichne die Strecke AC mit e=6 cm. Trage in A an AC einem Winkel mit dem Maß 12° an. Trage in C an CA einen Winkel mit dem Maß 12° an. Nenne den Schnittpunkt der freien Schenkel M. Zeichne einen Kreis um M durch A. Zeichne eine Parallele zu AB im Abstand 2 cm. Nenne einen der Schnittpunkte des Kreises mit der Parallelen B. Fälle das Lot von B auf AC und verlängere es über AC hinaus. Zeichne einen Kreis um B mit dem Radius f=4 cm. Nenne den Schnittpunkt des Kreises mit dem Lot D. Zeichne die Strecken AB, BC, CD und DA. ABCD ist das gesuchte Drachenviereck.

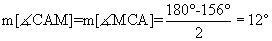
Fehlende Größen:
a=d=5 cm
b=c=2,5 cm
α = 47°
γ = 109°