Konstruiere ein Sehnenviereck aus a=6,3 cm; b=5 cm; c=7 cm; α=115°

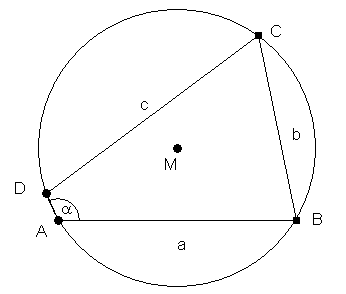
Da ABCD ein Sehnenviereck ist, gilt:
γ= 180° - α = 65°

Zeichne die Strecke BC mit b=5 cm. Trage in C an CB einen Winkel mit dem Maß γ=65° an. Zeichne einen Kreis um C mit dem Radius c=7 cm. Nenne den Schnittpunkt des Kreises mit dem freien Schenkel D. Errichte die Mittelsenkrechte zu BC. Errichte die Mittelsenkrechte zu CD. Nenne den Schnittpunkt der Mittelsenkrechten M und zeichne einen Kreis um M durch B. Zeichne einen Kreis um B mit dem Radius a=6,3 cm. Nenne einen der Schnittpunkt der Kreise A. Zeichne die Strecken AB und AD. ABCD ist das gesuchte Sehnenviereck.

Fehlende Größen:
d = 0,8 cm
β = 78°
γ = 65°
δ = 102°